 |
MQDS
0.0.1
Molecular Quantum Dynamics and Spectroscopy
|
 |
MQDS
0.0.1
Molecular Quantum Dynamics and Spectroscopy
|
The Partially Linearized Density Matrix (PLDM) propagation scheme is based off of a semiclassical path integral approximation to the propagator.
The time evolution of the expectation value of a general operator \( \langle \hat{O} \rangle(t) = \langle \Psi| e^{i H t} \hat{O} e^{-i H t} |\Psi \rangle \), where \( H \) is a general system-bath Hamiltonian and the system and bath are prepared in some initial state \( |\Psi\rangle \), can be accurately described using a semiclassical path integral formalism for the forward ( \( e^{-i H t} \)) and backward ( \( e^{i H t} \) ) propagators. Employing the Meyer-Miller mapping model to a general system-bath Hamiltonian in the diabatic representation, the discrete quantum states of the system are exactly mapped onto a set of fictitious harmonic oscillator raising and lowering operators ( \( |\alpha \rangle \rightarrow \hat{a}^\dagger_\alpha=(\hat{x}_{\alpha} - i \hat{p}_{\alpha})/\sqrt{2} \) ) and the Hamiltonian takes the form
\[ \hat{H}=\frac{\hat{P}^2}{2M} + \frac{1}{2}\sum_{\alpha} H_{\alpha \alpha}(\hat{R})\left( \hat{x}_\alpha^2 + \hat{p}_\alpha^2 -1 \right) + \frac{1}{2} \sum_{\beta \ne \alpha} H_{\alpha \beta}(\hat{R}) \left( \hat{x}_\alpha \hat{x}_\beta + \hat{p}_\alpha \hat{p}_\beta \right) \]
where \( \{ \hat{x}_{\alpha}, \hat{p}_{\alpha} \} \) and \( \{ \hat{P}, \hat{R} \} \) represent the complete sets of system and bath phase-space operators, respectively, and we take \( \hbar = 1 \).
To arrive at the partial linearized operator dynamics algorithm, the Herman-Kluk (or coherent state) semiclassical propagator is employed for the system DOFs. While results are independent of the specific choice of the coherent state width parameter, \( \gamma \), choosing it as \( \gamma=\frac{1}{2} \) has the useful consequence that the coherent state version of the semiclassical van Vleck determinant exactly cancels the troublesome \( -\frac{1}{2}\sum_\alpha H_{\alpha\alpha}(R) \) term in the Hamiltonian given above. This mitigates the issue of the bath DOFs propagating on an inverted potential energy surface (PES) when the mapping variables sample regions of phase space in which \( \hat{x}_\alpha^2 + \hat{p}_\alpha^2 < 1 \). The bath part of the full propagator is written in a phase space path integral form. Next, the phases of the path integral expressions for full forward and backward propagators are combined and the bath phase space DOFs are transformed to mean and difference variables, defined as \( \bar{R} = \left(R + R^\prime \right) /2 \) and \( Z = R - R^\prime \), respectively, with similar definitions for the corresponding momenta, \( \bar{P} \) and \( Y \). The approximation made in the partial linearization scheme, to this so far exact result, comes through a truncation of the functional Taylor series expansion about the mean bath phase space path, \( (\bar{R}(t), \bar{P}(t)) \) , to linear order in the difference path variables, \( Z(t) \) and \( Y(t) \). This approximation is based on the assumption that forward and backward nuclear paths will remain close to each other for short times. Upon functional integration of this partial linearized approximate result over bath difference path variables (e.g. \( Z_0\dots Z_{N-1} \) ), the final expression for the evolution of a matrix element of operator \( \hat{O} \) is obtained as
\[ \begin{split} \bigg\langle & n_t , \bar{R}_N + \frac{Z_N}{2} \bigg{|} \hat{O}(t) \bigg{|} n^\prime_t , \bar{R}_N - \frac{Z_N}{2} \bigg\rangle = \sum_{n_0,n_0^\prime} \int d\bar{R}_0 dx_0 dp_0 dx_0^\prime dp_0^\prime\ G_0 G_0' \\ & \times \frac{1}{2} ( x_{n_t} + ip_{n_t})(x_{n_0} - ip_{n_0}) \frac{1}{2} ( x^\prime_{n^\prime_t} - ip^\prime_{n^\prime_t} )( x^\prime_{n^\prime_0} + ip^\prime_{n^\prime_0} ) \left( \prod_{k=1}^{N-1} \int d\bar{R}_k \frac{d\bar{P}_k}{2\pi}\right) \int \frac{d\bar{P}_N}{2\pi} \\ & \times O_W^{n_0 n_0^\prime}(\bar{R}_0,\bar{P}_1) \ e^{i \bar{P}_NZ_N} \prod_{k=1}^{N-1}\delta\left( \frac{\bar{P}_{k+1}-\bar{P}_k}{\epsilon} - F_k \right) \prod_{k=1}^{N}\delta\left( \frac{\bar{R}_{k}-\bar{R}_{k-1}}{\epsilon} - \frac{\bar{P}_k}{M} \right) \end{split} \]
This equation should be interpreted in the following way: initial nuclear DOFs are sampled from the quasi-probability distribution (the so-called partial Weyl symbol) \( O_W^{n_0 n_0^\prime}(\bar{R}_0,\bar{P}_1) = \int dZ_0 \langle n_0,\bar{R}_0 + \frac{Z_0}{2} | \hat{O} | n^\prime_0,\bar{R}_0 - \frac{Z_0}{2} \rangle e^{-i\bar{P}_1Z_0} \), labeled by initial system states \( n_0 \) and \( n_0' \), and mapping variables (system DOFs) are sampled from the Gaussian functions \( G_0=\mathrm{exp}\left[{-\frac{1}{2}\sum_\alpha \left( x_{\alpha0}^2 + p_{\alpha0}^2 \right)}\right] \) and \( G_{0}^{\prime} \). The system mapping DOFs are evaluated along classical-like trajectories (satisfying Hamilton's Equations for the Hamiltonian given above) and the nuclear trajectories (as prescribed by the products of \( \delta \)-functions) are determined by an effective force \( F_k = - \frac{1}{2}\nabla_{\bar{R}_k}\big(\tilde{H}(\bar{R},x,p)+\tilde{H}(\bar{R},x^\prime,p^\prime)\big) \) resulting from different forward, \( (x,p) \), and backward, \( (x',p') \), system DOFs, where \( \tilde{H}(\bar{R},x,p)=\frac{1}{2}\sum_{\alpha}H_{\alpha\alpha}(\bar{R})(x_\alpha^2 + p_\alpha^2)+\frac{1}{2}\sum_{\alpha,\beta}H_{\alpha\beta}(\bar{R})(x_\alpha x_\beta + p_\alpha p_\beta) \). The trajectories propagated from such initial conditions provide a dynamical ensemble over which quantities can be averaged thus performing the following integrals \( \sum_{n_0,n_0^\prime} \int d\bar{R}_0 dx_0 dp_0 dx_0^\prime dp_0^\prime \), yielding the desired time evolved operator matrix elements. It should be pointed out that, although the Herman-Kluk propagator is semiclassical, the Meyer-Miller Hamiltonian is at most quadratic in the system mapping variables. Therefore, this semiclassical propagator provides an exact quantum mechanical treatment of the system dynamics for fixed bath variables.
This framework offers a robust and systematically improvable means of computing the time evolution of quantum mechanical operators. Indeed, the measure of quantum mechanical accuracy can be controlled by a simple repartitioning of the system-bath Hamiltonian. However, the necessity of averaging the (often oscillatory) complex phase factors associated with the product of polynomial terms in the mapping variables in the PLDM equation can be problematic, resulting in considerable noise in computed averages at longer times requiring larger ensembles of trajectories to obtain desired convergence. Alternatively, treating this algorithm as a short-time propagator where the linearization approximation is valid introduces quantum interference effects in the bath and, in the limit of infinite time slices, converges to exact quantum mechanical results.
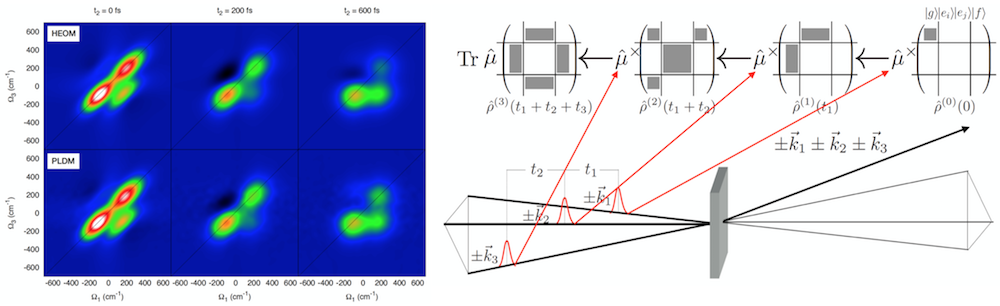
We can also use the PLDM propagator in conjunction with the focusing procedure to compute nonlinear electronic spectra!
Reference List:
 1.8.14
1.8.14